【論文読み】Non-local Neural Networks
2021年11月2日
FAIRのTimeSformerを読んだので、関連研究のNon-local Neural Networksを確認する。
忙しい人向け
どんな論文か
- 動画像間の長距離の依存性を捉えるためのnon-local 演算を提案。
先行研究と比べてどこがすごい
- CNN,RNNのように局所的な特徴量を捉えるのではなく、大域的に長距離の依存性を捉えることができる。
技術の手法やキモ
- ノイズ除去の古典的な手法であるnon-local means 法にヒントを得て、ある位置での応答をすべての位置での特徴の加重和として計算する。
- 多くのCVのアーキテクチャに組み込むことができる。

どうやって有効だと検証した
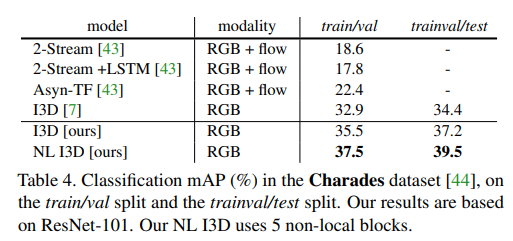
- Kinetics datasetとCharades datasetの両方で、以前のSOTAモデルと競い合ったり、凌駕する結果を得た。
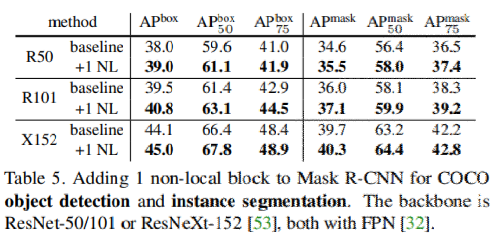
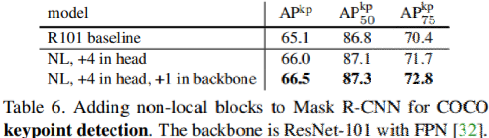
- 静止画認識では、COCOタスクでobject detection, segmentation, pose estimationを向上。
議論はあるか
- 既存動画処理モデル(I3D対応モデル)よりも長い動画シーケンスに有効である。table2(g)参照
モデルの詳細
non-localの利点
- RNN,CNNの漸進的動作とは対照的に、位置の距離に関係なく、任意の2つの位置間の相互作用を計算することで、長期依存性を直接捉えることができる。
- 実験で示すようにnon-local演算は効率的であり、わずか数層(例えば5層)での最良の結果を得ることができる。
- 3DCNNよりも計算量が少なくてすむ
Non-local Neural Networks
Formulation
既存研究のnon-local mean 演算に従ってnon-local 演算を次のように定義する。
$y_i = \frac{1}{C(x)} \sum_{\forall j}f(x_i, x_j)g(x_j) (1)$
- i: outputを計算する位置(空間、時間、時空)のindex
- j: 可能なすべての位置を列挙するindex
- x: 入力信号(画像、シーケンス、動画、それらの特徴)
- y: xと同じサイズの出力信号
- f: iとすべてのjの間のスカラー(親和性などの関係を表す)を計算する関数
- g: 位置jにおける入力信号の表現を計算する単項関数。
全結合層との違い
- 全結合層
- 学習した重みを使用。$x_i$と$x_j$の関係は、全結合では入力データの関数ではない。
- 固定サイズの入力が必要。
- 位置の対応関係が失われる。
- DNNの最終層に使用されることが多い。
- non-local 式(1)
- 異なる場所間の関係に基づいてoutputを計算
- 可変サイズの入力に対応、対応するサイズをoutputに保持。
- 柔軟な構成要素であり、CNN,RNNとの併用も容易
- DNNの初期に追加可能。
インスタンス化
fとgのいくつかのバージョンについて説明する
簡略化のため、gは線形埋め込みの形でのみ考える。
$g(x_j) = W_{g}x_j$
- $W_g$は、学習する重み行列(空間における1×1の畳み込みや時空間における1x1x1の畳み込みとして実装)
Gaussian
pairwise関数のfの選択についてガウス関数を使用
$f(x_i, x_j) = e^{x_i^T x_j} (2)$
- $x_i^T x_j$はdot積の類似性(ユークリッド距離も適用可能だがdot積のほうが実装しやすい)
正規化関数は以下のように設定
$C(x) = \sum_{ \forall j} f(x_i, x_j)$
Embedded Gaussian
ガウス関数の簡単な拡張は、埋め込み空間での類似性を計算することである。
$f(x_i, x_j) = e^{\theta(x_i)^T \phi (x_j)}(3)$
- $\theta(x_i) = W_{\theta}x_i$(埋め込み)
- $\phi(x_i) = W_{\phi}x_j$(埋め込み)
- $C(x) = \sum_{ \forall j} f(x_i, x_j)$
self-attentionはembedded gaussian におけるnon-local 的な操作の特殊なケース。与えられたiに対して、$\frac{1}{C(x)} f(x_i, x_j)g(x_j) $が次元jに沿ったsoftmax計算になることからわかる。
$y=softmax(x^T W^T_{\theta}W_{\phi}x)g(x)$
となり、これがself-attention型となる。
この研究では古典的なCVの手法であるnon-local的手法と関連付けることで洞察を与え、Ashish Vaswaniらの逐次self-attention ネットワークをCVにおける静止画、動画認識のための一般的な時空間non-local ネットワークに拡張している。softmaxによるattentionの振る舞いは必須ではないことを示すためにnon-local的操作の2つの代替バージョンを説明する。
- Dot product
- fはdot積の類似性として次のように定義できる
- $f(x_i, x_j) = \theta(x_i)^T \phi (x_j) (4)$
- 正規化係数を$C(x)=Nとする$
- Nはfの総和ではなく、xの位置数(勾配計算を簡単にするため)
- embedded gaussianとの違いは活性化関数のsoftmaxの存在
- Concatenation
- Relation networksのpairwise関数で視覚的推論に用いられている。
- fの連結形式を評価すると以下のようになる
- $f(x_i, x_j)= ReLU(w^T_f[\theta(x_i),\phi(x_j)]) (5)$
- $[..]$は連結を表す
- $w_f$は連結されたベクトルをスカラに投影する重みベクトル
- $C(x)= N$
- fにReLUを採用
Non-local Block
式1のnon-local演算を、既存の多くのアーキテクチャに組み込むことが可能なnon-local vlockにまとめる。定義は以下の通り。
$z_i = W_z y_i + x_i(6)$
- y_iは式(1)で与えられ、"$+x_i$"は残差接続を表す。
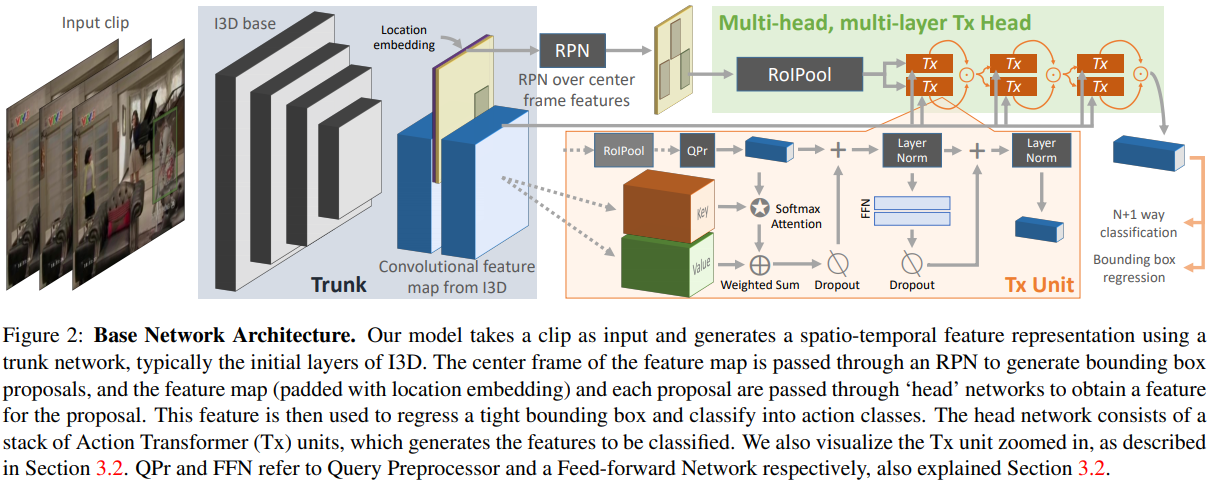
fig2にnon-local blockの例を示す。
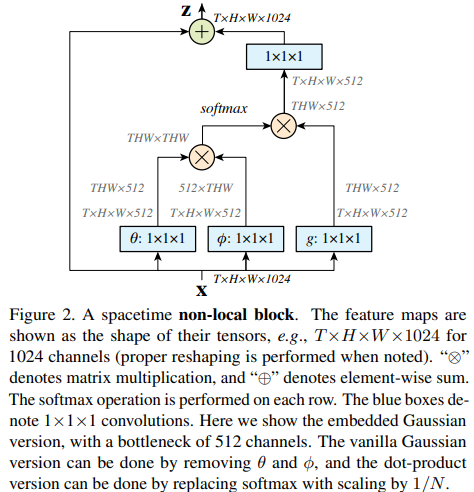
- 式(2),(3),(4)のpair-wise計算は、fig2に示すように、単純に行列の乗算で行う。
- 典型的な値は、$T=4, H=W=14 or 7$
より効率的にするために以下のような実装を採用
Impremantation of Non-local Blocks
- $W_g, W_{\theta}, W_{\phi}$で表されるチャンネル数をxのチャンネル数の半分に設定する。(計算量を半分にできる)
- 式(6)の重み行列$W_z$は$y_i$のいちごとの埋め込みを計算し、チャンネル数をxのそれに合わせる(fig2参照)
- 式(1)を次のように修正して、サブサンプリングという手法を用いる。
- $y_i = \frac{1}{C(\hat{x})} \sum_{\forall _j} f(x_i, \hat{x}_j)g(\hat{x}_j)$
- $\hat{x}$は$x$のサブサンプリングされたバージョン(pooling等によって)
- これを空間領域で行うことでpair-wiseの計算量を1/4削減できる。(non-localな動作を変えるものではなく、計算をより粗くするもの)
- fig2の$\phi$と$g$の間にmax pooling層を追加することで可能
本論文ではすべてのnon-local blockにこれらの修正を加えている。
baselineモデルとしてC3D,I3Dを使用。non-local blocを適用して実験を行った。
結果

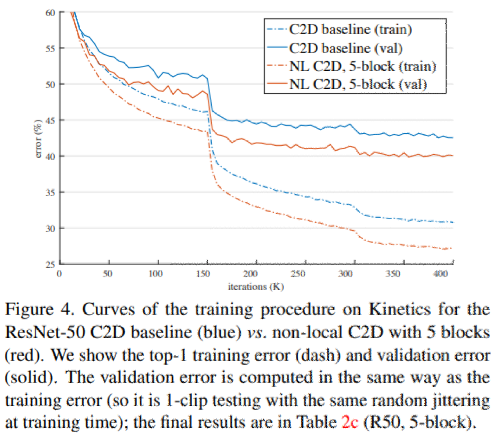
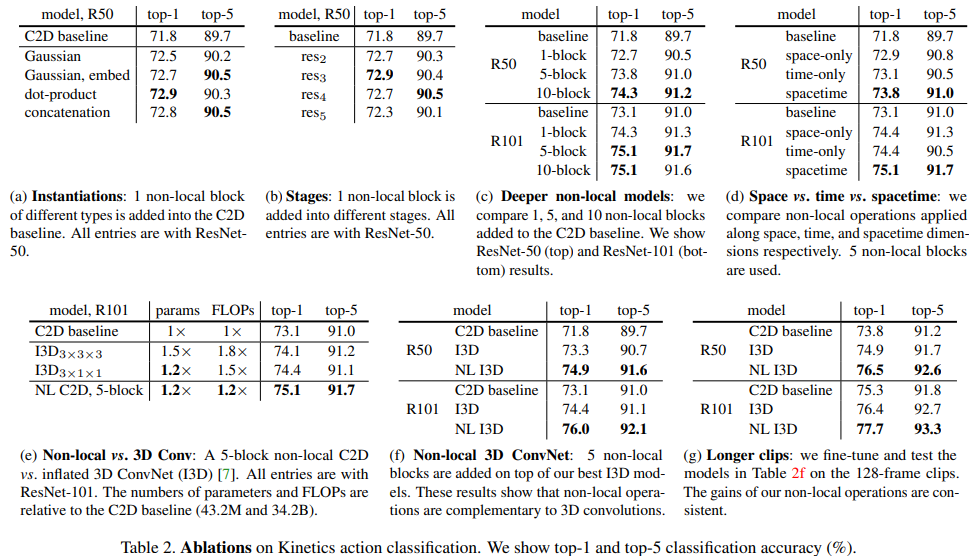
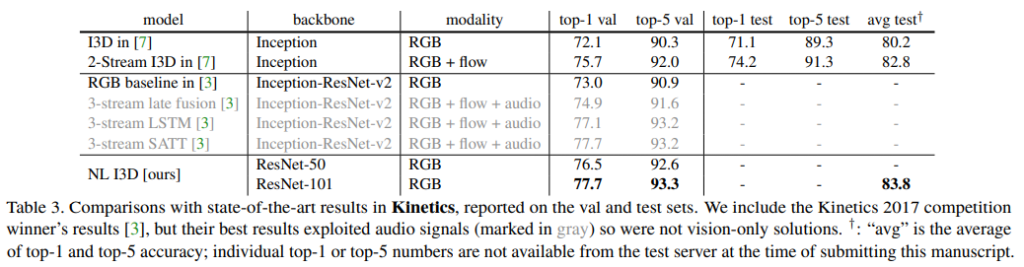
論文AI,Attention,deeplearning,Dot product,Embedded Gaussian,non-local,non-local block,Non-local Neural Networks,self-attention,transformer,video,動画,動画処理
Posted by kazu
関連記事
【論文読み】MoViNets: Mobile Video Networks for Efficient Video Recognition 日本語まとめ
CVPR2021, Google ReserchのDan Kondratyukさ ...
【論文読み】TimeSformer論文解説まとめ
論文 Is Space-Time Attention All You Need ...
【論文読み】ViViT: A Video Vision Transformer 日本語まとめ
忙しい人向け どんな論文か Transformerだけを用いた動画分類モデルを提 ...
【論文読み】Video Action Transformer Network, まとめ
FAIRのTimeSformerの論文を読んだので、関連研究で紹介されていたVi ...
【論文読み】Pay Attention to MLPs 日本語まとめ
Pay Attention to MLPsを読んだ。GooleResearchの ...


ディスカッション
コメント一覧
まだ、コメントがありません